机器学习基础 ¶

机器学习基础 ¶

线性回归 ¶

• 一维：\(\hat{y} = wx + b\)
• N 维：\(\hat{y} = \mathbf{w}^\top\mathbf{x} + b\)
• 损失函数：\(l^{(i)}(\mathbf{w}, b) = \dfrac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2\)
• 梯度下降法求解参数

梯度下降 ¶

• \(L(\mathbf{w}, b) = \sum_il^{(i)}(\mathbf{w}, b)\)
• 用 \((\mathbf{w}, b)-\eta\nabla L(\mathbf{w}, b)\) 代替 \((\mathbf{w}, b)\)
• 学习率 \(\eta\)，超参数（用来控制学习），下降的快慢
  • 学习率过大会在最优附近横跳
  • 学习率过小则太慢
  • 根据进度更改学习率
    • Linear Decay
    • Linear Warmup：先小，然后增大，再缓慢变小

SGD¶

Minibatch Stochastic Gradient Descent

• 随机采用一部分样本来计算损失函数
• \(L(\mathbf{w}, b) = \sum_{i\in B}l^{(i)}(\mathbf{w}, b)\)
• Batch size \(s=|B|\) 也是一个超参数
  • \(s\) 小，工作量小，拟合效果不好
  • \(s\) 大，内存消耗高

深度学习基础 ¶

多层感知器 ¶

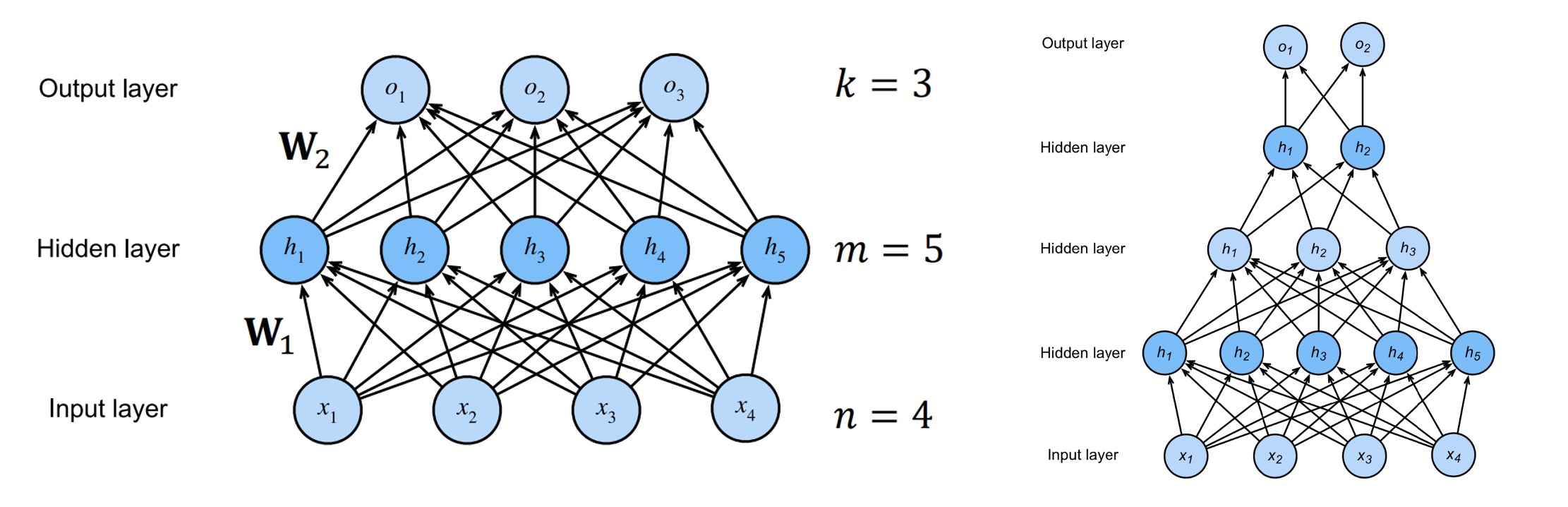
多层感知器（Multilayer Perceptrons， MLP）是一种前向结构的人工神经网络，结构例如：

• 输入层（Input Layer）：\(\mathbf{x}\in\mathbb{R}^n\)
• 隐藏层（Hidden Layer）：\(\mathbf{h} = \sigma(\mathbf{W_1x}+\mathbf{b_1})\)
  • \(\mathbf{W_1}\in\mathbb{R}^{m\times n}, \mathbf{b_1}\in\mathbb{R}^m, \mathbf{h}\in\mathbb{R}^m\)
  • \(\sigma\)：激活函数（activation function）
  • 可以有很多隐藏层，逐层传递
• 输出层（Output Layer）：\(\mathbf{o} = \mathbf{W_2h}+\mathbf{b_2}\)
  • \(\mathbf{W_2}\in\mathbb{R}^{k\times m}, \mathbf{b_2}\in\mathbb{R}^k, \mathbf{o}\in\mathbb{R}^k\)
• 结果：\(\mathbf{\hat{y}}=\sigma_2(\mathbf{o})\)

前向传播（Forward Propagation）¶

按顺序从输入层开始计算，得到每一层的输出结果

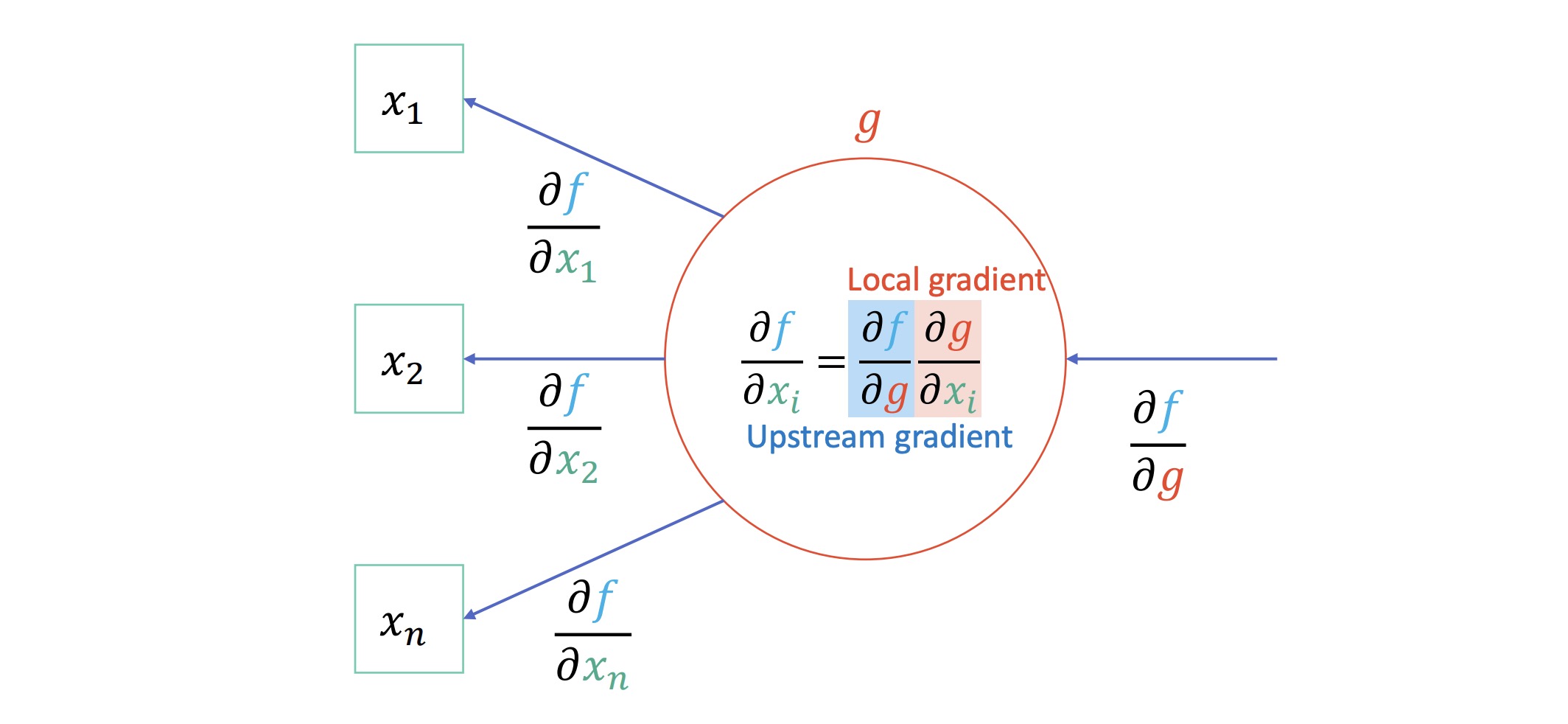
反向传播（Back Propagation）¶

利用链式法则来计算神经网络中各参数的梯度

激活函数 ¶

没有激活函数的情况：

• \(\mathbf{h} = \mathbf{W_1x}+\mathbf{b_1}\)
• \(\mathbf{o} = \mathbf{W_2h}+\mathbf{b_2} = \mathbf{W_1W_2x}+\mathbf{b_1}+\mathbf{b_2}\) 仍为线性的

而激活函数使得 \(\mathbf{h} = \sigma(\mathbf{W_1x}+\mathbf{b_1})\)，让 MLP 变为非线性的

一些激活函数：

• sigmoid：\(\text{sigmoid}(x) = \dfrac{1}{1+e^{-x}}\)，导数：\(\text{sigmoid}(x)(1-\text{sigmoid}(x))\)
• tanh：\(\tanh(x) = \dfrac{1-e^{-2x}}{1+e^{-2x}}\)，导数：\(1-\tanh^2(x)\)
• ReLU：\(\text{ReLU}(x)=\max(x, 0)\)
  • Rectified Linear Unit
  • 屏蔽掉负值
• softmax：\(\text{softmax}(\mathbf{o})_i = \dfrac{e^{o_i}}{\sum_{j=1}^ke^{o_j}}\)
  • 将输出的值转化为概率（和为 1）

规范化 ¶

#TODO，PPT 55-59 页，没懂

优化算法 ¶

SGD：\(W\leftarrow W-\eta\nabla L(W)\)

SGD + Momentum¶

SGD 只依赖当前 batch 计算得到的梯度来更新，不稳定。在梯度下降过程中加入动量，累积历次计算的梯度，使之更稳定，而且防止陷入局部最优解

• \(v\leftarrow \rho v+\nabla L(W)\)
  • \(v\)："velocity"，累积的梯度
  • \(\rho\)："friction"，动量因子，一般为 0.9 或 0.99
• \(W\leftarrow W-\eta v\)

AdaGrad¶

设置全局学习率之后，每次通过全局学习率逐参数的除以历史梯度平方和的平方根使得每个参数的学习率不同

在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度

• \(s\leftarrow s+(\nabla L(W))^2\)
  • \(s\)：累积平方梯度
  • 平方是逐元素相乘
• \(W\leftarrow W-\dfrac{\eta}{\sqrt{s}+\epsilon}\nabla L(W)\)
  • \(\epsilon\)：为了维持数值稳定性，一般为 \(10^{-6}\) 或 \(10^{-7}\) 之类小常数

Adam¶

对梯度的一阶矩估计（First Moment Estimation，即梯度的均值）和二阶矩估计（Second Moment Estimation，即梯度的未中心化的方差）进行综合考虑，计算出更新步长，效果更好

• 迭代次数记为 \(i=1, \dots, n\)
• \(v\leftarrow \beta_1v+(1-\beta_1)\nabla L(W)\)
• \(s\leftarrow \beta_2s+(1-\beta_2)(\nabla L(W))^2\)
• Bias correction：\(v'=\dfrac{v}{1-\beta_1^i}, s'=\dfrac{s}{1-\beta_2^i}\)
• \(W\leftarrow W-\eta\dfrac{v'}{\sqrt{s'}+\epsilon}\)
• 一般情况下通常设 \(\beta_1=0.9, \beta_2=0.999, \eta=10^{-3}\) 或 \(5\times 10^{-4}\)

卷积神经网络 ¶

卷积神经网络（Convolutional Neural Network，CNN）是一类强大的、为处理图像数据而设计的神经网络

卷积 ¶

一维卷积：

离散形式：

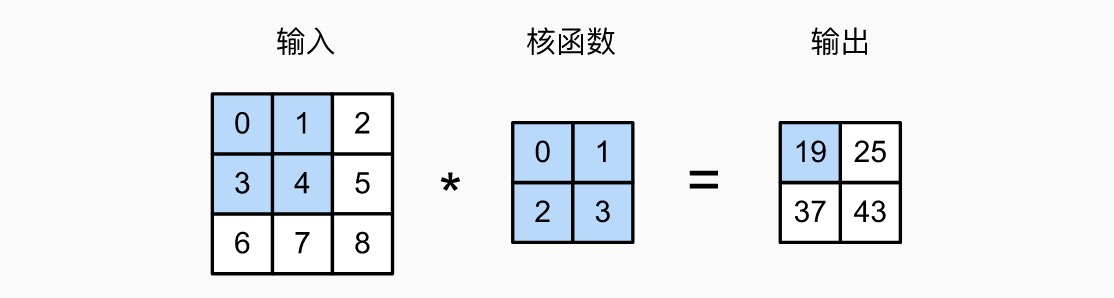
二维离散卷积：

图像卷积 / 互相关（cross-correlation）

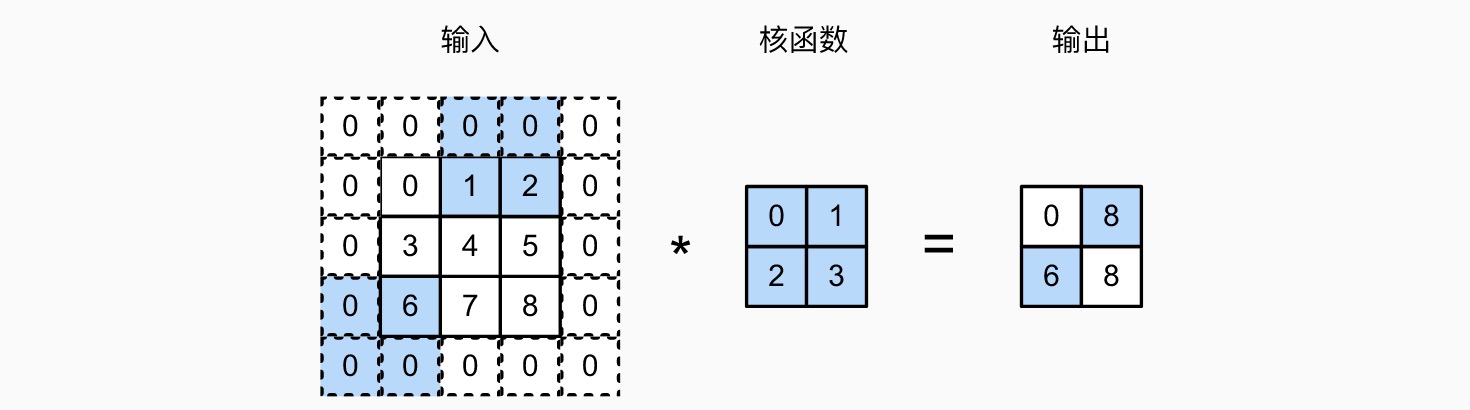
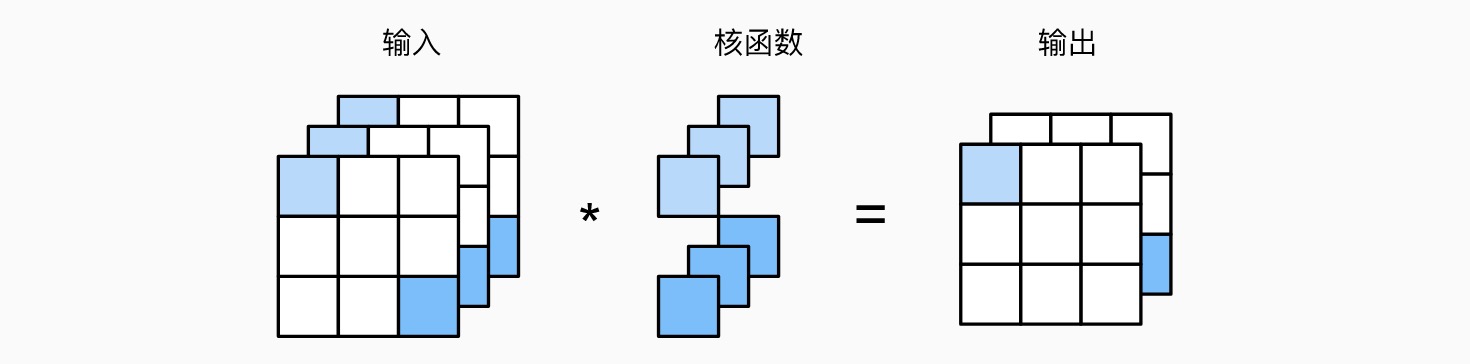
带 padding 的二维卷积

• 在周围填充
• 可以填充 0，也可以填充临近的数

带步幅（stride）的二维卷积（下图水平步幅为 2，垂直步幅为 3）

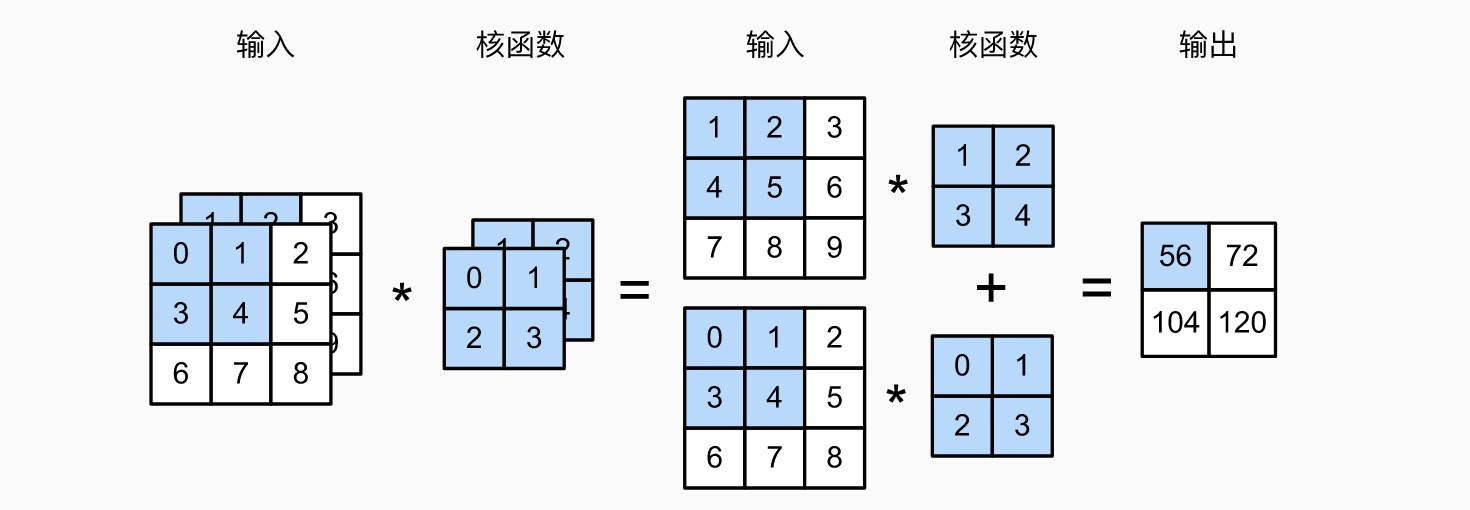
多通道卷积（会降维）

多输出通道卷积（如图为 \(1\times 1\) 卷积）

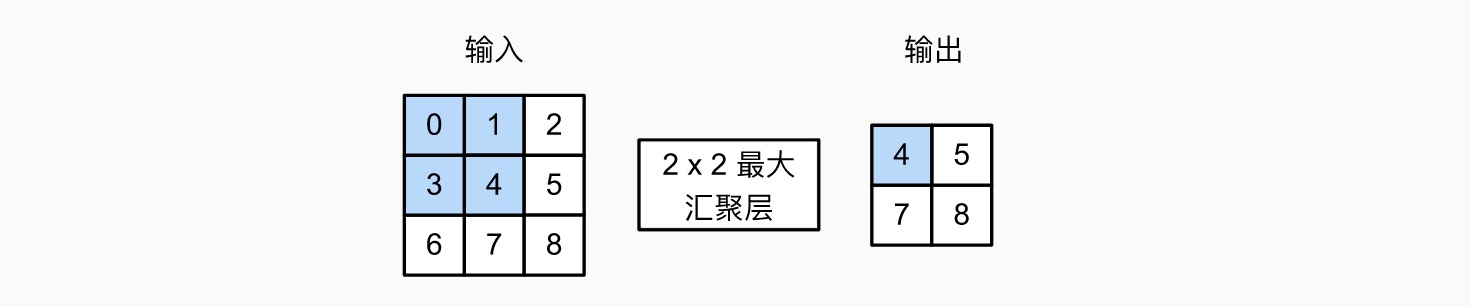
汇聚（池化）¶

池化即 pooling，与卷积层类似，只是不进行乘法操作，也不需要核，只是通过窗口划分区域，然后做加法 / 取最大值 / 取平均。例如最大汇聚层：

汇聚层作用：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性

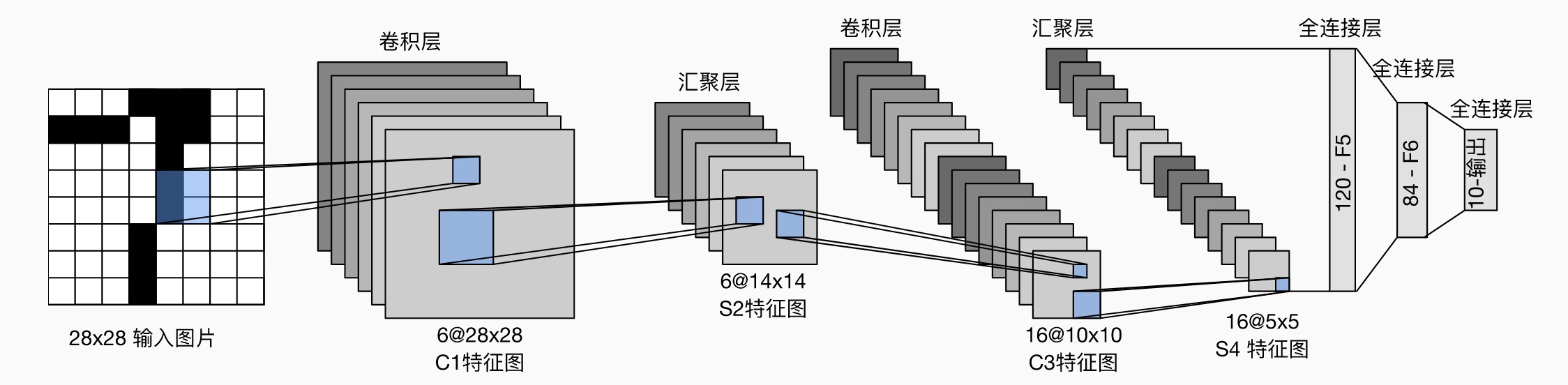
LeNet¶

1989 年提出的 CNN 模型（LeNet-5），用来从 28*28 的输入图片中识别数字，结构：

包含两个部分：

• 卷积编码器：每个卷积块是一个卷积层（5*5 卷积核，padding 为 2），一个 sigmoid 激活函数，一个平均汇聚层（2*2 池，stride 为 2）
  • 第一层有 6 个通道，第二层有 16 个通道
• 全连接层密集块：有三个全连接层（中间是 sigmoid 激活函数）
  • 三个全连接层输出个数依次为 120、84、10（最终 10 个数字）

现代卷积神经网络 ¶

AlexNet¶

和 LeNet 结构和设计理念类似。输入一个 224*224 带三通道的图片，输出识别出的物体类别（一共 1000 种），结构：

图片（3*224*224）-> 11*11 卷积层（96 通道，stride 4）-> 3*3 最大汇聚层（stride 2）-> 5*5 卷积层（256 通道，padding 2）-> 3*3 最大汇聚层（stride 2）-> 3*3 卷积层（384 通道，padding 1）-> 3*3 卷积层（384 通道，padding 1）-> 3*3 卷积层（256 通道，padding 1）-> 3*3 最大汇聚层（stride 2）-> 全连接层（输出 4096）-> 全连接层（输出 4096）-> 全连接层（输出 1000）

激活函数使用 ReLU

VGG¶

使用了更小的卷积核（3*3）和 2*2 的最大汇聚层，有更深的层级（16-19 层）

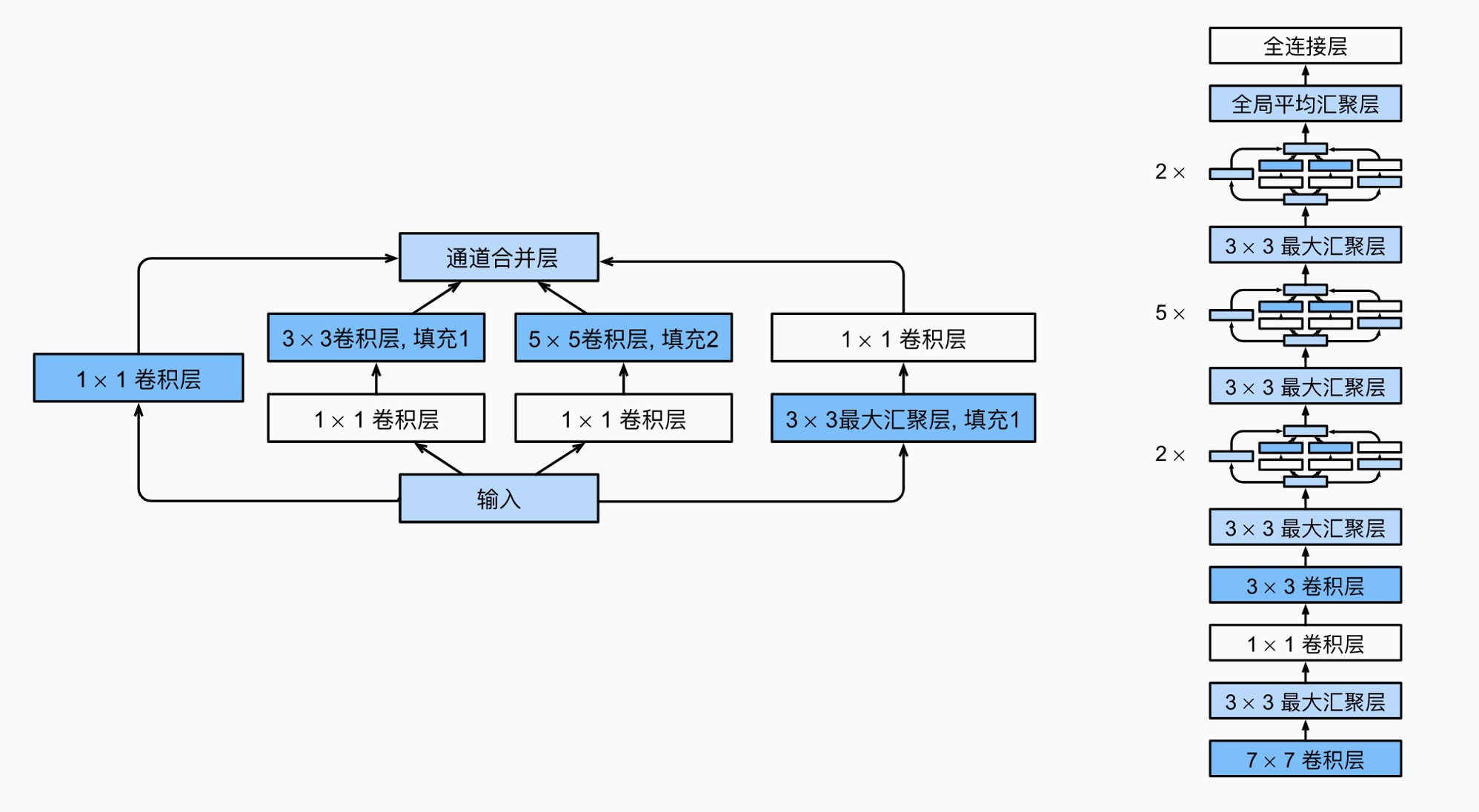
GoogLeNet¶

使用了 Inception 块：

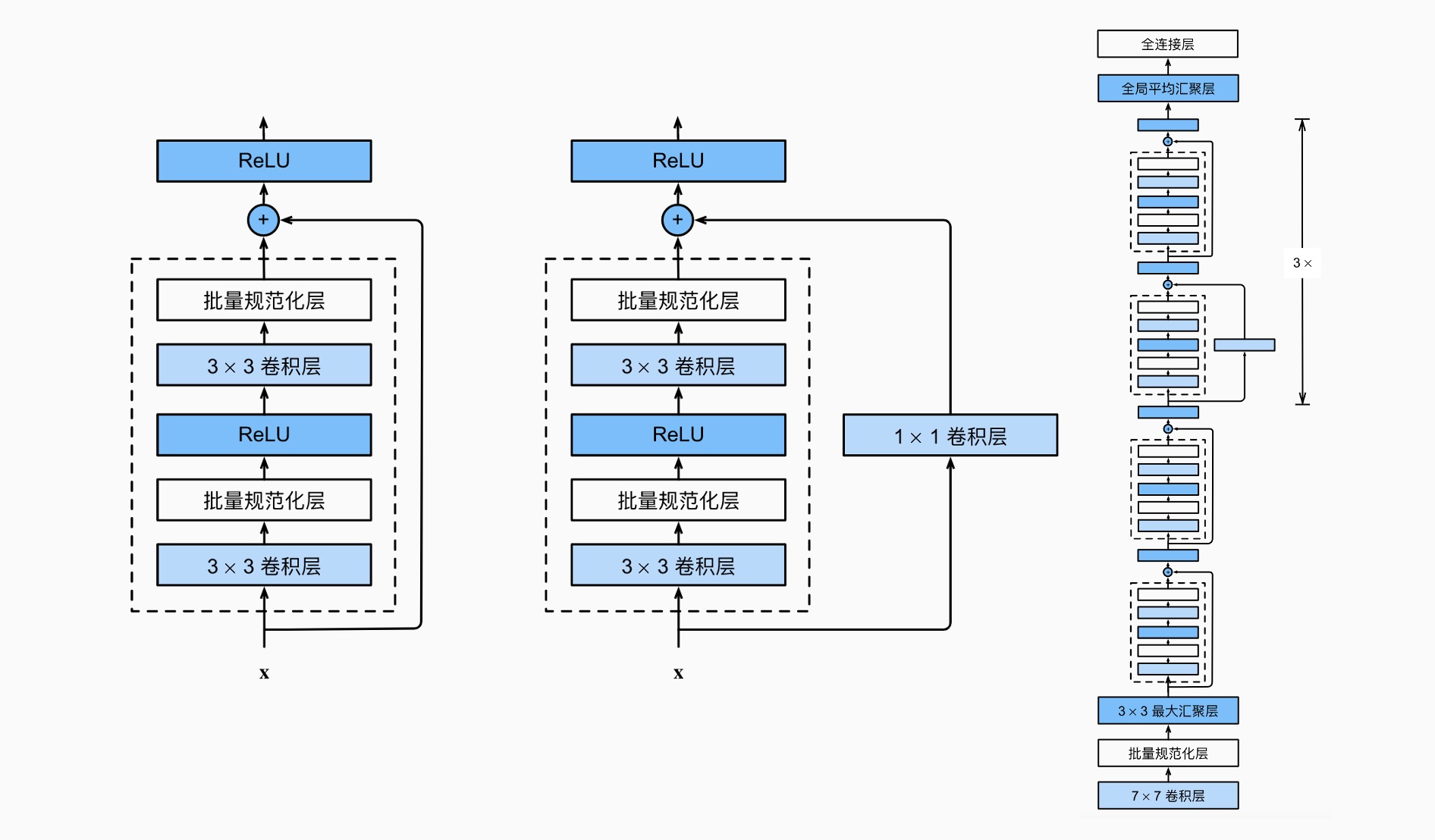
ResNet¶

即残差网络，使用了残差块，学习 \(f(x)-x\) 来确保 \(\mathcal{F}_i\subset\mathcal{F}_{i+1}\)，逐次收敛到 " 真实 " 函数 \(f^*\)

迁移学习 ¶

迁移学习（Transfer Learning）是指在原有数据集训练好参数后，更换数据集时只需要重新训练全连接部分

• 对于小数据集，仅初始化全连接输出层并重新训练，固定其它层参数，只改变全连接输出层参数
• 对于大数据集，仅初始化全连接输出层和全连接隐藏层，固定其它层参数，重新训练

循环神经网络 ¶

循环神经网络（Recurrent Neural Network，RNN）可以更好地处理序列信息

这里本应有更多内容，但是懒得写了 _(:з」∠)_