二维码 QRCode 标准阅读 ¶
约 6170 个字 13 行代码 16 张图片 预计阅读时间 21 分钟
最近几次比赛遇到过好几次二维码的题目,打算好好来读一读标准文档 ISO/IEC 18004:2015 文档 6.1 前面的内容不多,就从它后面开始记了
基础描述及结构(6.1、6.3)¶
基础描述(5.3、6.1)¶
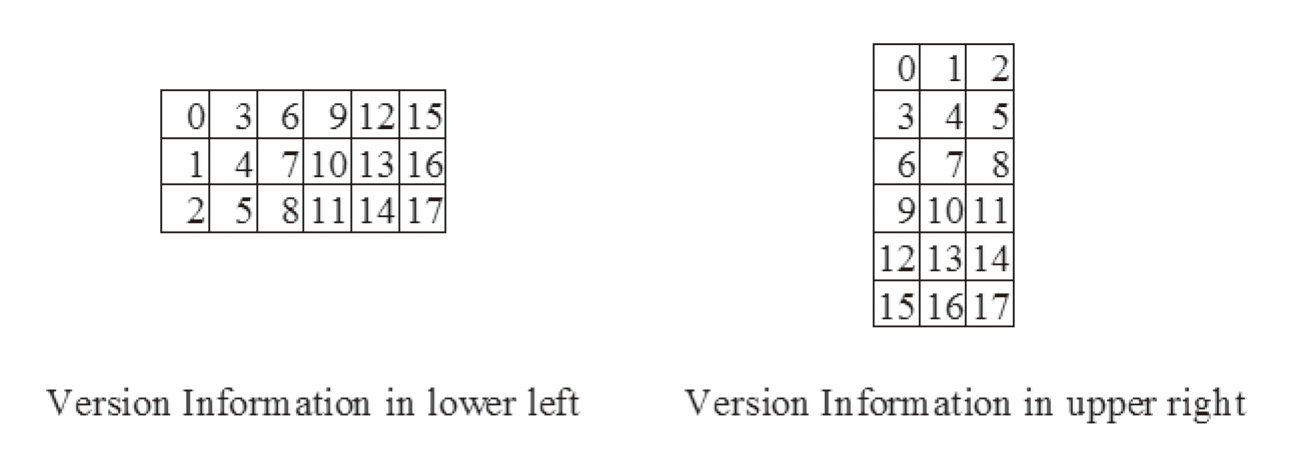
- 块位置:左上角为原点 (0, 0) 向下 x+,向右 y+
- 版本表示:Version V-E(其中 V 是版本号,E 是纠错等级)
- 数据表示:黑块 -1 白块 -0(可以带背景全部反色)
- 大小:从版本 1 到版本 40 依次是 21x21 ~ 177x177(每增加一个版本,边长增加 4)
- 支持的最多字符数(版本 40)
- 数字模式:7089
- 字母模式:4296
- 字节模式:2953
- 日文模式:1817
- 纠错等级允许的恢复比例
- L:7%
- M:15%
- Q:25%
- H:30%
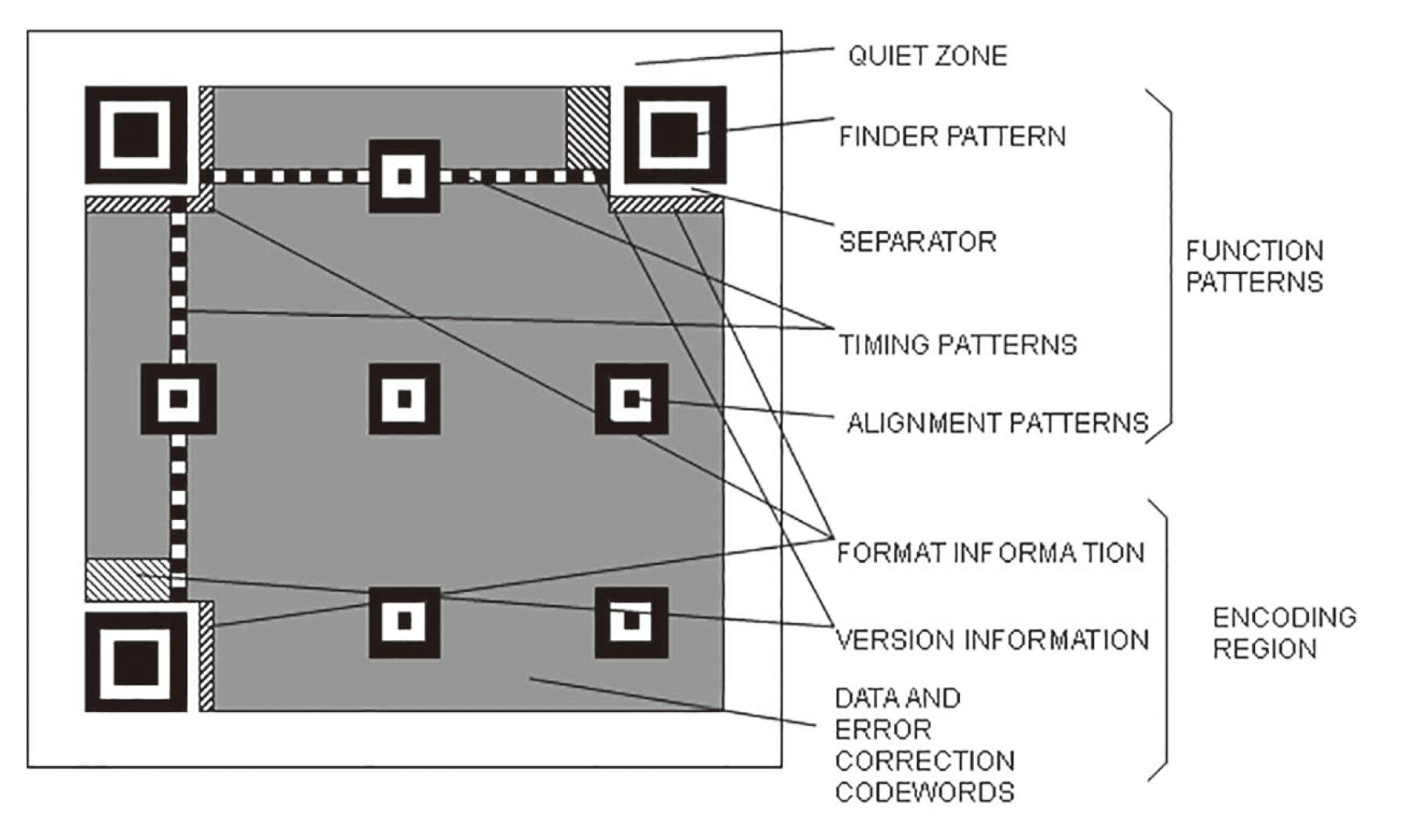
二维码结构(6.3)¶
- 功能图案(function patterns)
- 特征符(finder pattern)7x7 黑圈 5x5 白圈 3x3 黑块
- 分割线(separator)在特征符周围的一圈全白区域
- 时序图案(timing patterns)第 7 行第 7 列的两条黑白条纹
- 对齐图案(alignment patterns)版本 1 无,版本 2-6 1 个,版本 7-13 6 个……(附录 E)
- 静默区(quiet zone)至少 4 个单位宽
- 编码区域(encoding region)
- 格式信息(format information)左上角分割线外一圈,左下角分割线右侧,右上角分割线下侧
- 版本信息(version information)版本 7 后才有,在左下分割线上侧,右上分割线左侧
- 数据及纠错码区域
数据编码(7.4)¶
数据序列(7.4.1)¶
默认的 ECI 模式下,比特流以模式标识符开始。如果不是默认 ECI 模式,则需要从 ECI 头开始:
- (4 bits)ECI 模式标识符
- (8/16/24 bits)ECI Designator
比特流的剩余部分由下面几部分组成:
- (4 bits)模式标识符
- 字符数量标识符(长度见下第二个表)
- 数据比特流
| 模式 | 标识符 | 说明 |
|---|---|---|
| ECI | 0111 | |
| 数字模式 | 0001 | 只包含数字 0-9,3 个数字 10 bits |
| 字母数字模式 | 0010 | 45 个字符,0-9A-Z 及 9 个符号 空格 $%*+-./:,2 个字符 11 bits |
| 字节模式 | 0100 | 每个字符 8 bits |
| 日本汉字模式 | 1000 | |
| 结构添加模式 | 0011 |
| 版本 | 数字模式字符数量标识符长度 | 字母模式…… | 字节模式…… | 日文模式…… |
|---|---|---|---|---|
| 1~9 | 10 | 9 | 8 | 8 |
| 10~26 | 12 | 11 | 16 | 10 |
| 27~40 | 14 | 13 | 16 | 12 |
ECI 模式(7.4.2)¶
ECI 模式即使用某些特定的字符映射来把字符转换为比特流
而且都使用字节模式来表示数据(即在 ECI 头后的模式标识符为字节模式的 0100)
每个 ECI 都有一个六位数编号(assignment value
| ECI Assignment Value | Codewords values |
|---|---|
| 000000 ~ 000127 | 0xxxxxxx |
| 000000 ~ 016383 | 10xxxxxx xxxxxxxx |
| 000000 ~ 999999 | 110xxxxx xxxxxxxx xxxxxxxx |
而且 ECI 模式下中途可以更换 ECI 指示器,一个 5C(01011100)表示换新的 ECI,后面要接 6 个 codewords 即 6 个数字(十六进制 30~39)表示编号,而不是用上表中的表示方法。而 5C 正常情况下表示 ,所以表示 这个原数据需要用两个 5C
例子 1
使用 ISO/IEC 8859-7(ECI 000009)来表示希腊字母 ΑΒΓΔΕ(该 ECI 下表示为十六进制 A1 A2 A3 A4 A5)
比特流:
- ECI 标识符:
0111 - ECI 编号:
00001001 - 字节模式标识符:
0100 - 字符数量
: 00000101(5 个字符) - 数据:
10100001 10100010 10100011 10100100 10100101
所以最终的比特流:0111 00001001 0100 00000101 10100001 10100010 10100011 10100100 10100101
例子 2(14.3)
- 需要编码的数据:ABC\123456
- 数据流中十六进制(字节模式标识符 0100 后
) :41 42 43 5C 5C 31 32 33 34 35 36
- 数据流中十六进制(字节模式标识符 0100 后
- 需要编码的数据:ABC< 后接 ECI 123456 下的数据……>
- 数据流中十六进制(字节模式标识符 0100 后
) :41 42 43 5C 31 32 33 34 35 36 ……
- 数据流中十六进制(字节模式标识符 0100 后
数字模式(7.4.3)¶
输入的数字字符串(因为开头可以是 0)要被分成 3 个一组,每组会转换为 10 bits 的二进制串(999 -> 11111001111100011)如果剩 1 个数字,则将其转换为 4 bits 的二进制串(9 -> 1001)
然后开头加上数字模式标识符 0001 和数量标识符(字符个数转为二进制,并开头补 0 至长度,长度由版本决定,见上 7.4.1 部分的第二个表)
例子
- 数据内容:
01234567(保留开头 0) - 数据流部分:
- 数字模式标识符:
0001 - 数量标识符:
0000001000(8,且版本 1 下规定为 10 bits) - 数据:
- 012 ->
0000001100 - 345 ->
0101011001 - 67 ->
1000011
- 012 ->
- 数字模式标识符:
- 完整数据比特流:
0001 0000001000 0000001100 0101011001 1000011
数字模式下的比特流长度为:
其中 M 为 4,C 为数量标识符长度(版本 1~9 为 10,版本 10~26 为 12,版本 27~40 为 14
字母数字模式(7.4.4)¶
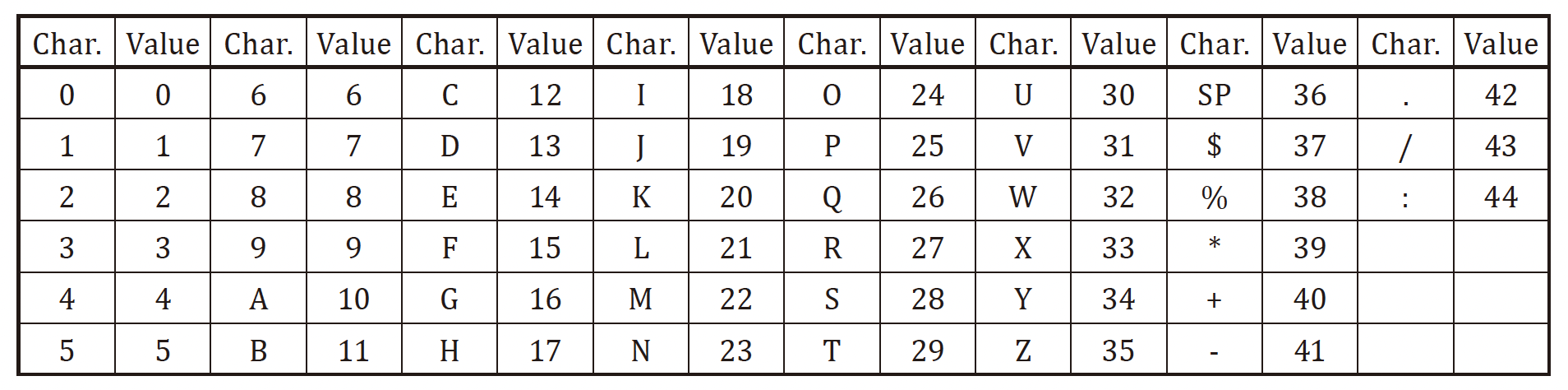
数字字母模式(Alphanumeric mode)下支持的编码字符有 45 个,把它们从 0 编号至 44。其中 0-9 对应数字 0-9,10-35 对应字母 A-Z,36-44 对应 9 个符号:
输入的字符先按照上表转换为数值,然后分为两个一组,每一组内把 第一个数值 × 45 + 第二个数值,再转换为长度为 11 bits 的二进制串(最大为 44×45+44=2024 -> 11111101000101100)
然后开头加上字母数字模式标识符 0010 和数量标识符(长度由 7.4.1 第二个表规定)
例子
数据内容:AC-42
数据流部分:
- 字母数字模式标识符:
0010 - 数量标识符:
000000101(5,且版本 1 下规定长度为 9) - 数据:AC-42 -> 10 12 41 4 2 -> (10 12)(41 4)(2)
- 10 12 -> 10*45+12=462 ->
00111001110 - 41 4 -> 41*45+4=1849 ->
11100111001 - 2 -> 2 ->
000010
- 10 12 -> 10*45+12=462 ->
完整数据比特流: 0010 000000101 00111001110 11100111001 000010
字母数字模式下的比特流长度为:
其中 M 为 4,C 为数量标识符长度,D 为原数据长度
字节模式(7.4.5)¶
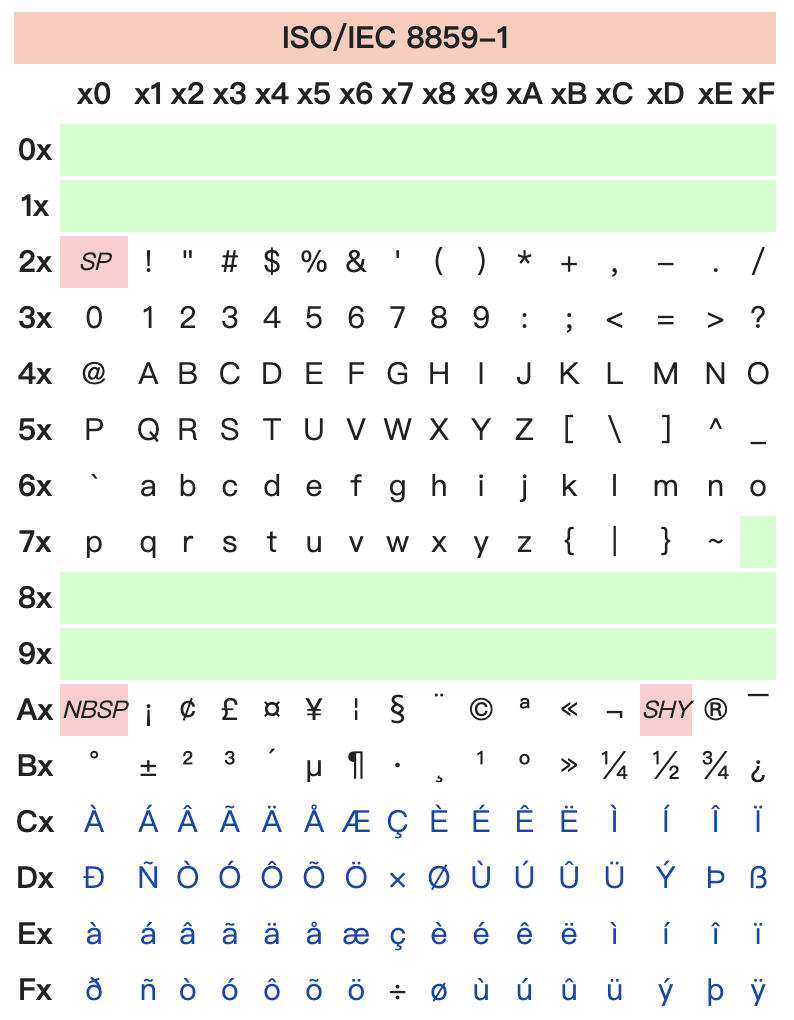
字节模式(Byte mode)下把每个字符根据 Latin-1(ISO/IEC 8859-1)编码成 8 bits(1 字节0100 和数量标识符(长度由 7.4.1 第二个表规定)的后面。
字节模式下的比特流长度:
其中 M 为 4,C 为数量标识符长度,D 为原数据长度
中文编码 ¶
中文在转换成比特流的时候也使用字节模式,需要用 UTF-8 编码,每个字符会被编码成 3 个字节
混合模式(7.4.7)¶
一个二维码的数据流中也可以使用多种模式,且不需要特别表示。更换新的模式时只需要正常添加 模式标识符 + 数量标识符 + 数据 即可
例子
原始数据:123 测试
数据流:
- 数字模式:
- 标识符:
0001 - 数量标识符:
0000000011(3,长度 10) - 数据:123 ->
0001111011
- 标识符:
- 字节模式:测试 -> E6 B5 8B / E8 AF 95
- 标识符:
0100 - 数量标识符:
00000110(6,长度 8) - 数据:
- 测 ->
11100110 10110101 10001011 - 试 ->
11101000 10101111 10010101
- 测 ->
- 标识符:
完整数据比特流: 0001 0000000011 0001111011 0100 00000110 11100110 10110101 10001011 11101000 10101111 10010101
结束符(7.4.9)¶
在数据的末尾要填充 4 个 0 作为结束符,如果容量不足的话可以缩短或省略 即能填下则加4个0,填不下则能加几个0就加几个0
填充 padding bits(7.4.10)¶
转换后的数据比特流还需要填充至二维码的数据容量
- 首先先用
0补充比特流长度到 8 的整数倍 - 然后用
11101100和00010001交替填补到二维码数据容量
具体的数据容量由版本号和纠错等级决定,且数据容量(比特)一定为 8 的倍数,完整数据见文档的 33~36 页(整个 pdf 的第 41~44 页)
注
这个地方 QRazyBox 网站存在 bug,有时无法正常识别填充的 0 比特和 padding bits(即可能把填充的 0 中前四个视为一个 terminator,把后面的 0 才视为属于 padding bits )
纠错码编码(7.5)¶
纠错容量(7.5.1)¶
纠错字(error correction codewords)可以纠正两种错误,一种是比如无法扫描或无法解码的已知位置的错误字(erasures
可以纠错的 erasures 和 errors 的数量满足:
其中 \(e\) 是 erasures 的数量,\(t\) 是 errors 的数量,\(d\) 是纠错字的数量,\(p\) 是被错误解析的保护字数量
其中 \(p\) 由版本决定:
- \(p=3\):版本 1-L
- \(p=2\):版本 1-M、2-L
- \(p=1\):版本 1-Q、1-H、3-L
- \(p=0\):其他所有版本
分块编码纠错码 ¶
根据版本号及纠错等级,数据序列需要被分成 1 个或多个块,每块内需要单独编码纠错码
如果需要补充的话一律全部补充 0 比特到需要的长度
具体不同版本的分块块数和每块中数量安排以及纠错容量都在文档中 P38-44(pdf 中 P46-52)的大表格 Table 9 中
生成纠错码(7.5.2)¶
伽罗瓦域 ¶
生成纠错码之前要先将所有数据字转换成一个多项式,使其限制于伽罗瓦域 \(GF(2^3)\bmod 100011101\) 中,而且后续的四则运算也都是该伽罗瓦域中的运算
具体伽罗瓦域的生成原理可以看:https://www.codenong.com/cs105738710/
简单来说就是多项式的加减法都是异或,乘除法要每一个比特模 2,每一个字节模 100011101(即该伽罗瓦域中的本原多项式 \(x^8+x^4+x^3+x^2+1\))
具体多项式 mod 运算的方法可以看:https://blog.csdn.net/yaongtime/article/details/17200401
简单来说就是多项式的长除法取模,而且注意这里的加减都是伽罗瓦域中的加减,即异或
生成多项式(Annex A)¶
纠错码生成多项式的一般表达形式是:
其中 \(n\) 为纠错码字的个数,其中 \(\alpha=2\), \(\alpha^k\) 的是在伽罗瓦域下的运算,即:
\(\alpha^0 = 1;\ \alpha^1=2;\ \alpha^2=4;\ \cdots;\ \alpha^7=128\)
\(\alpha^8=256\bmod 285=256\oplus 285=29;\ \alpha^9=29\times2=58;\ \cdots\)
具体计算 \(\alpha^k\) 的代码:
文档附录 A 中已经展开了所有可能 \(n\) 值下的 36 个生成多项式
生成纠错码 ¶
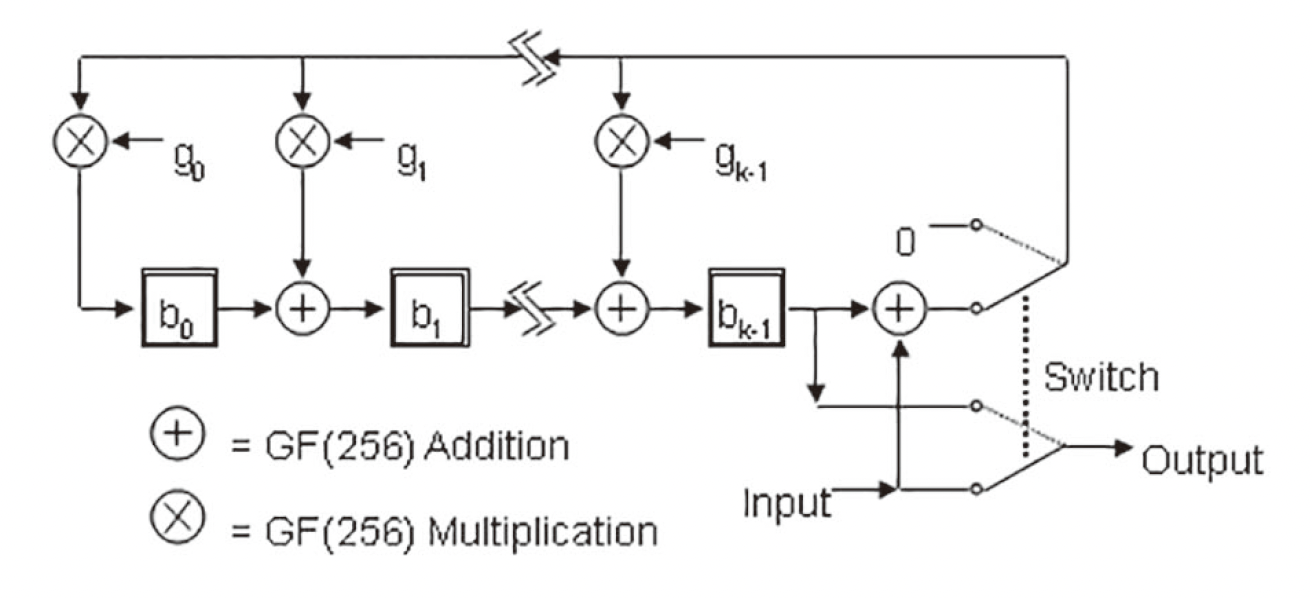
文档里给了一个感觉比较晦涩难懂的图来展示生成纠错码的过程:
不是很容易理解,于是找了另一篇文章:https://blog.csdn.net/ljm1995/article/details/88819664
举个例子,比如要编码 12345678 这八个数字
版本 1-L,查 Table 9 得到分为 1 块,且该块内总字数为 26,数据字数为 19,纠错字数为 26-19=7
根据前面所说,比特流应该是: 0001 0000001000 0001111011 0111001000 1001110 0000
补成 8 的倍数长度: 00010000 00100000 01111011 01110010 00100111 00000000
添加 padding bits(补到 19 个字节00010000 00100000 01111011 01110010 00100111 00000000 11101100 00010001 11101100 00010001 11101100 00010001 11101100 00010001 11101100 00010001 11101100 00010001 11101100
写成多项式形式,次数是 19 次,整体乘 \(x^7\):
再查附录 A 得到次数为 7 的生成多项式,并整体乘 \(x^{18}\):
然后把第一个多项式除第二个多项式取余数
可以这样计算,把第二个多项式整体乘 16 即 \(\alpha^4\):
计算出系数的值:
之后与第一个多项式异或得到:
这之后最高次就变成了 24 次,重复整个过程直到结果只剩下 7 项(即最高次为 6 次)时即可得到:
所以纠错码就是:188 247 62 248 53 170 224
转为二进制: 10111100 11110111 00111110 11111000 00110101 10101010 11100000
所以整个二维码的编码区域(除格式信息外)全部内容就是:
00010000 00100000 01111011 01110010 00100111 00000000 11101100 00010001 11101100 00010001 11101100 00010001 11101100 00010001 11101100 00010001 11101100 00010001 11101100 10111100 11110111 00111110 11111000 00110101 10101010 11100000
纠错码可以直接用 python 的 reedsolo 包来求解:
>>> from reedsolo import RSCodec, ReedSolomonError
>>> rsc = RSCodec(7)
>>> list(rsc.encode([16, 32, 123, 114, 39, 0, 236, 17, 236, 17, 236, 17, 236, 17, 236, 17, 236, 17, 236]))
[16, 32, 123, 114, 39, 0, 236, 17, 236, 17, 236, 17, 236, 17, 236, 17, 236, 17, 236, 188, 247, 62, 248, 53, 170, 224]
>>> list(rsc.encode([16, 32, 123, 114, 39, 0, 236, 17, 236, 17, 236, 17, 236, 17, 236, 17, 236, 17, 236]))[-7:]
[188, 247, 62, 248, 53, 170, 224]
剩余步骤(7.6~7.10)¶
合成序列(7.6)¶
首先按照 2 中所述给完整信息编码成数据序列,其中也包含 padding bits,且长度为 8 的倍数
然后根据 3.1.1 中所说对数据序列进行分块,然后对每块分别生成纠错码
最后把数据序列的所有块按照字节依次交错合成新的数据序列,然后把纠错码的所有块按照字节交错合成纠错码序列。把新的数据序列和纠错码序列连接在一起,如果总长度不够二维码的容量,则在后面补充 3/4/7 个 0 比特(需要补多少在 Table 1 中有定义)
而且这样也要保证最短的数据块在最前面(已经由 Table 9 定义)
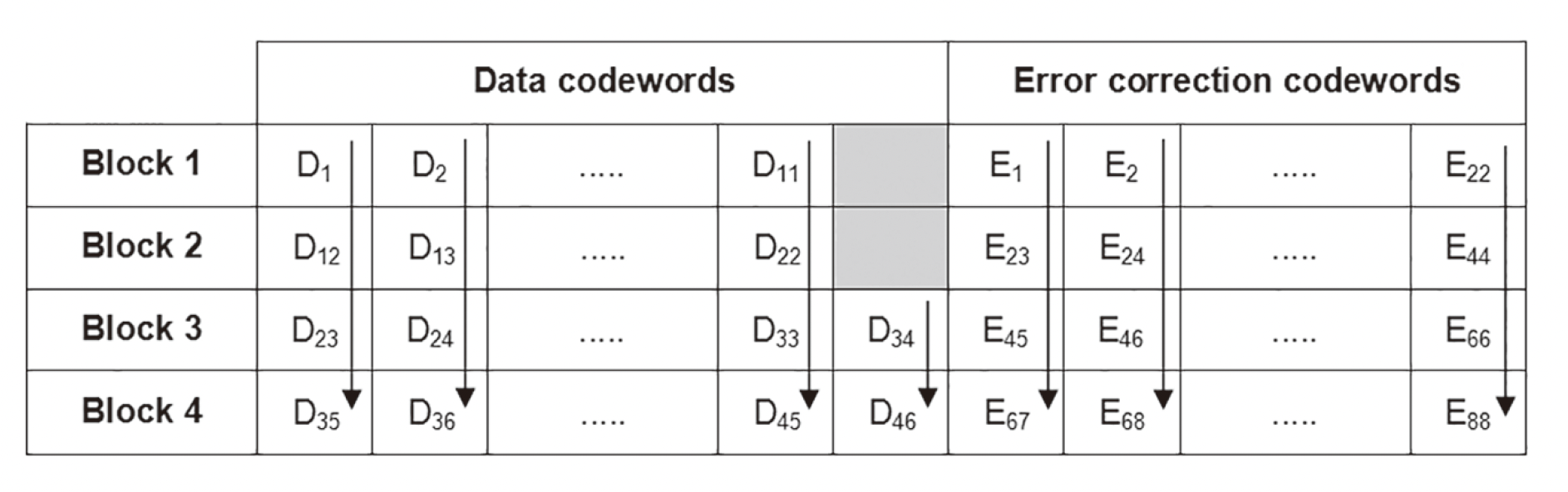
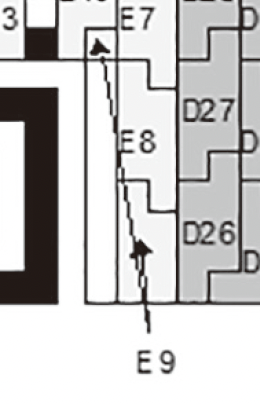
比如 5-H 版本的序列,需要分为 4 块,前两块是 11 个数据字、22 个纠错字,后两块是 12 个数据字、22 个纠错字:
最后的序列就是 \(D_1,D_{12},D_{23},D_{35},\cdots,D_{45},D_{34},D_{46},E_1,E_{23},\cdots,E_{88}\)
填充数据(7.7)¶
把前面合成的完整消息序列填到二维码中,首先要先填充功能图案,然后预留出格式信息、版本信息的位置
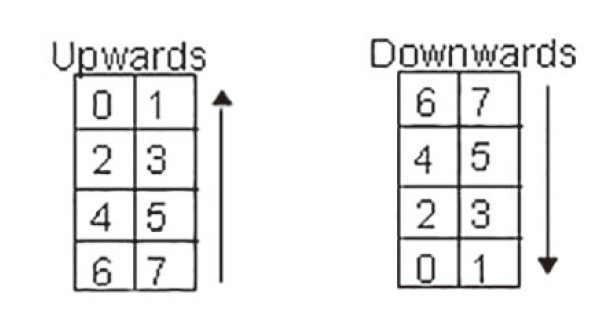
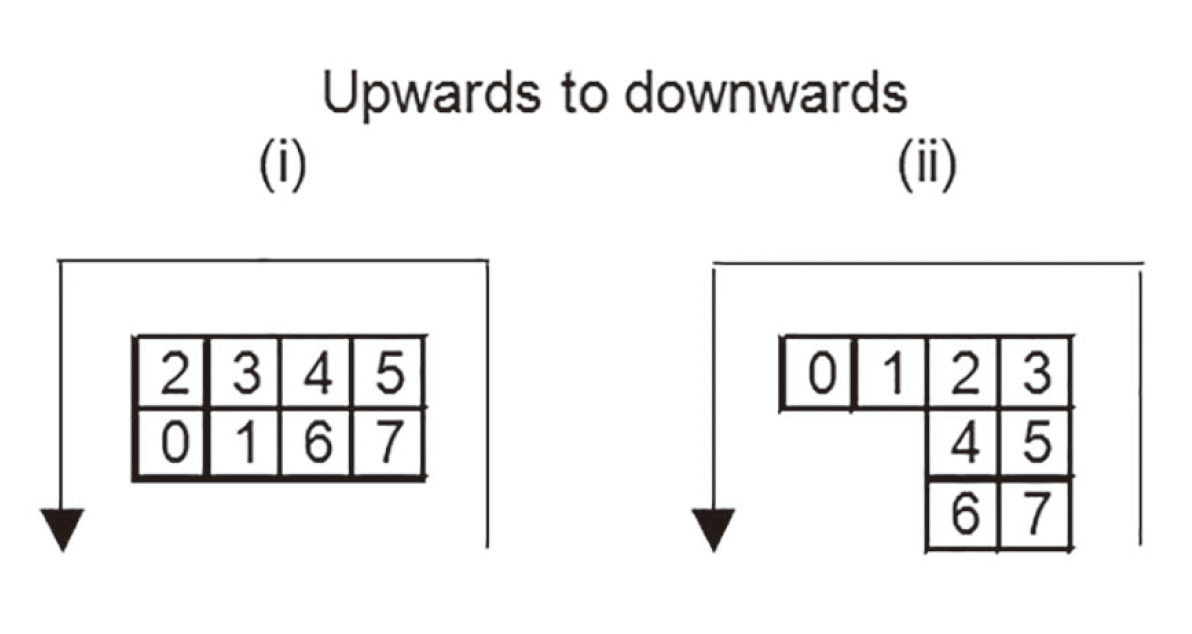
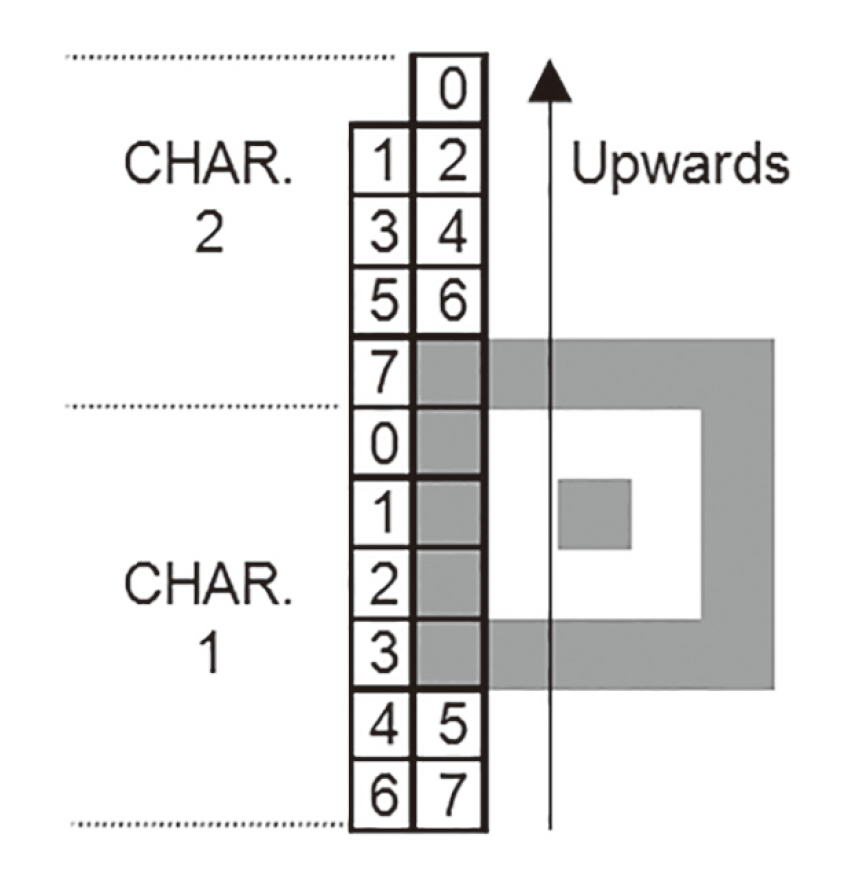
填充时以两列为单位,即每次交替填充两列。从最右下角开始是最高位的比特,然后从右向左从下向上交替填充,到了上界时左转向下继续填充,遇到对齐图案直接穿过,遇到对齐图案边界则变为一行
也可以按照字节来依次填充,如果是向上填充,则最高位在下端,反之在上段。每个字节块内的最高位尽量取最右侧的,但如果最下 ( 上 ) 端只有一个比特的位置,则选它作为最高比特的位置
反正按顺序正常填就行了,遇到东西就绕
掩码遮盖(7.8)¶
填充后的数据还要遮盖一层掩码(异或)来平衡黑白块的数量,以及减少容易产生扫描错误的大块和形似功能图案的部分出现
QR 码一共有 8 种掩码,每个掩码有一个 3 bits 的编号,和一个生成公式。这个公式用来生成掩码图样,以左上为原点,向右、下为正方向,坐标满足这个公式的点在图样中是黑色(1
进行掩码操作就是把除去功能图案和版本信息、格式信息之外的数据部分每一块的值与掩码图样异或
整个操作需要生成分别使用不同掩码的 8 个图样,然后计算出损失分数(penalty points score
计算损失分数(7.8.3)¶
虽然进行掩码操作时仅对非功能图案、非版本信息格式信息的数据区域进行掩码,但是计算损失分数时按照整个二维码计算
计算损失分有四个规则:
- 相邻一行或一列内出现连续五个相同颜色块时损失分 +3,之后连续块数每加一,损失分 +1
- 寻找内部颜色相同的 2*2 的块,每出现一个损失分 +3
- 在每行和每列中寻找
10111010000和00001011101,每出现一个损失分 +40 - 评估黑色块占全部块数的比例,如果在 45%~55% 间则不增加损失分,在 40%~45%、55%~60% 间则损失分 +10,在 35%~40%、60%~65% 间则损失分 +10*2,以此类推
更详细的例子可以看:https://www.thonky.com/qr-code-tutorial/data-masking
然后对所有掩码结果计算损失分数后选择分数最低的一个作为最终结果
格式信息(7.9)¶
QRCode 的格式信息是 15 bits 的序列,其中前 5 位是数据,后 10 位是针对格式信息的纠错码(由 (15, 5) BCH 码生成)
5 bits 的数据前 2 位是纠错等级标识符,分别是 L -> 01 、M -> 00 、Q -> 11 、H -> 10
后 3 位是上面说到的掩码编号
然后后接 10 bits 纠错码,最后整体异或 101010000010010 防止产生全零数据序列
生成纠错码(Annex C)¶
先得到前 5 bits 的数据,然后化为多项式,整体乘 \(x^{10}\),再除以生成多项式 \(G(x)=x^{10}+x^8+x^5+x^4+x^2+x+1\) 得到余数转换为后 10 bits 的纠错码
例子
- 纠错等级 M,掩码编号 101
- 5 bits 数据:
00101 - 写为多项式: \(x^2+1\)
- 整体乘 \(x^{10}\): \(x^{12}+x^{10}\)
- 除以 \(G(x)\): 商 \(x^2\),余数 \(x^7+x^6+x^4+x^3+x^2\)
- 余数转为 10 bits 纠错码:
0011011100 - 加上原数据:
001010011011100 - 异或
101010000010010:100000011001110
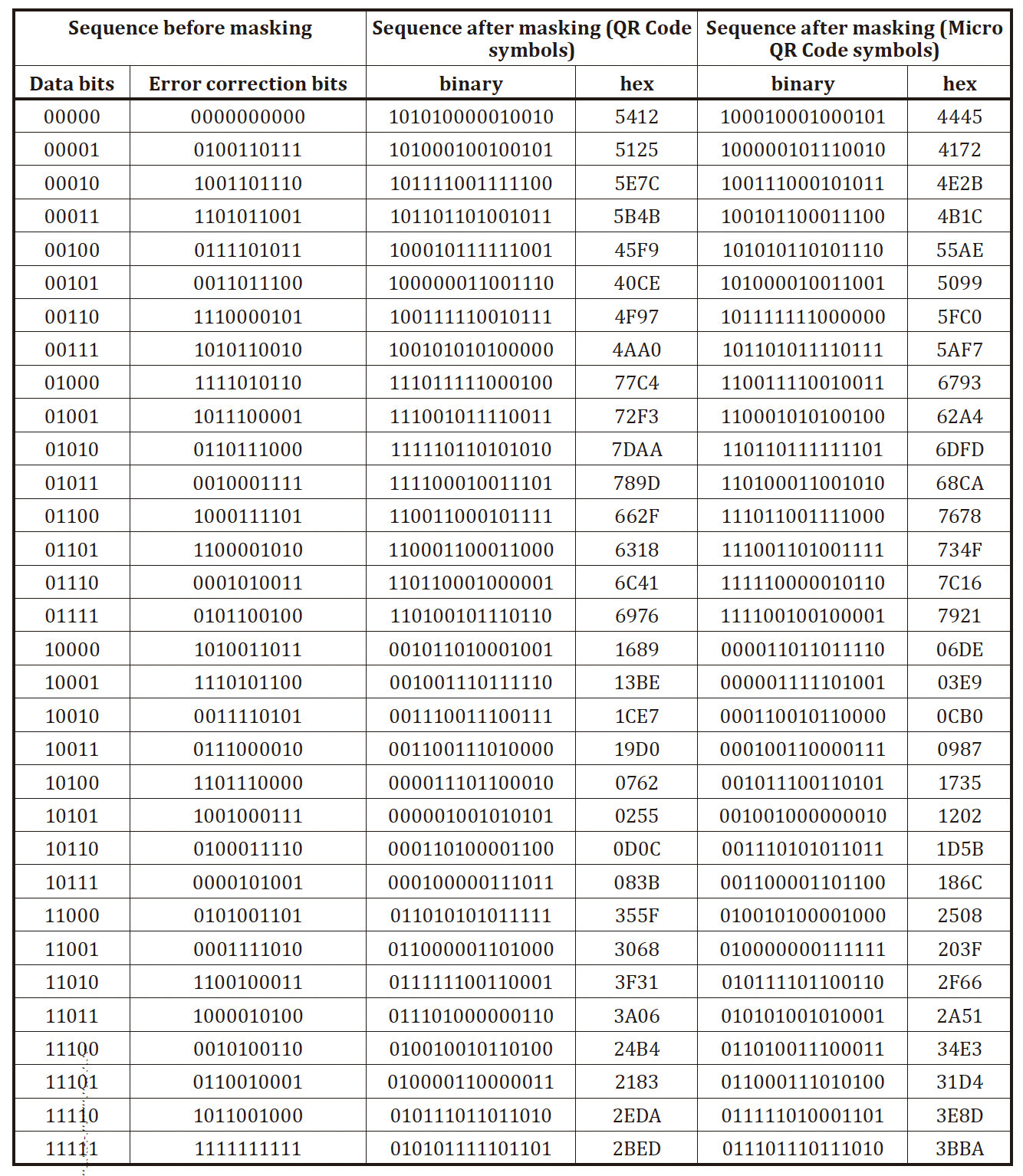
因为 5 bits 的数据一共只有 32 种情况,所以附录 C 中直接给出了完整的表格:
纠错:最多可以纠正 3 bits 的错误,先把格式信息异或 101010000010010 得到原始序列,然后与 Table C.1 中的有效格式信息进行对比,如果找不到说明有错误。此时仅选择 Table C.1 中与错误格式信息相差比特最少的一个作为纠正后的格式信息即可,如果相差少于等于 3 个比特,则视为纠正成功
填入二维码 ¶
左上角的格式信息区域填充一份完整的格式信息(最高位在左(4V+9,8))有一块始终是黑色:
版本信息(7.10)¶
在版本 7 及以上的二维码中需要填入版本信息来确保准确度
版本信息只储存了该二维码的版本号(7~40000111 到 101000
不同于格式信息,因为版本号不会出现全零,所以不需要进行掩码操作
生成纠错码(Annex D)¶
和格式信息的纠错码类似,先把前 6 bits 转为多项式,然后整体乘 \(x^{12}\),得到的结果除以生成多项式 \(G(x)=x^{12}+x^{11}+x^{10}+x^9+x^8+x^5+x^2+1\) ,把余数转为 12 bits 二进制就是纠错码了
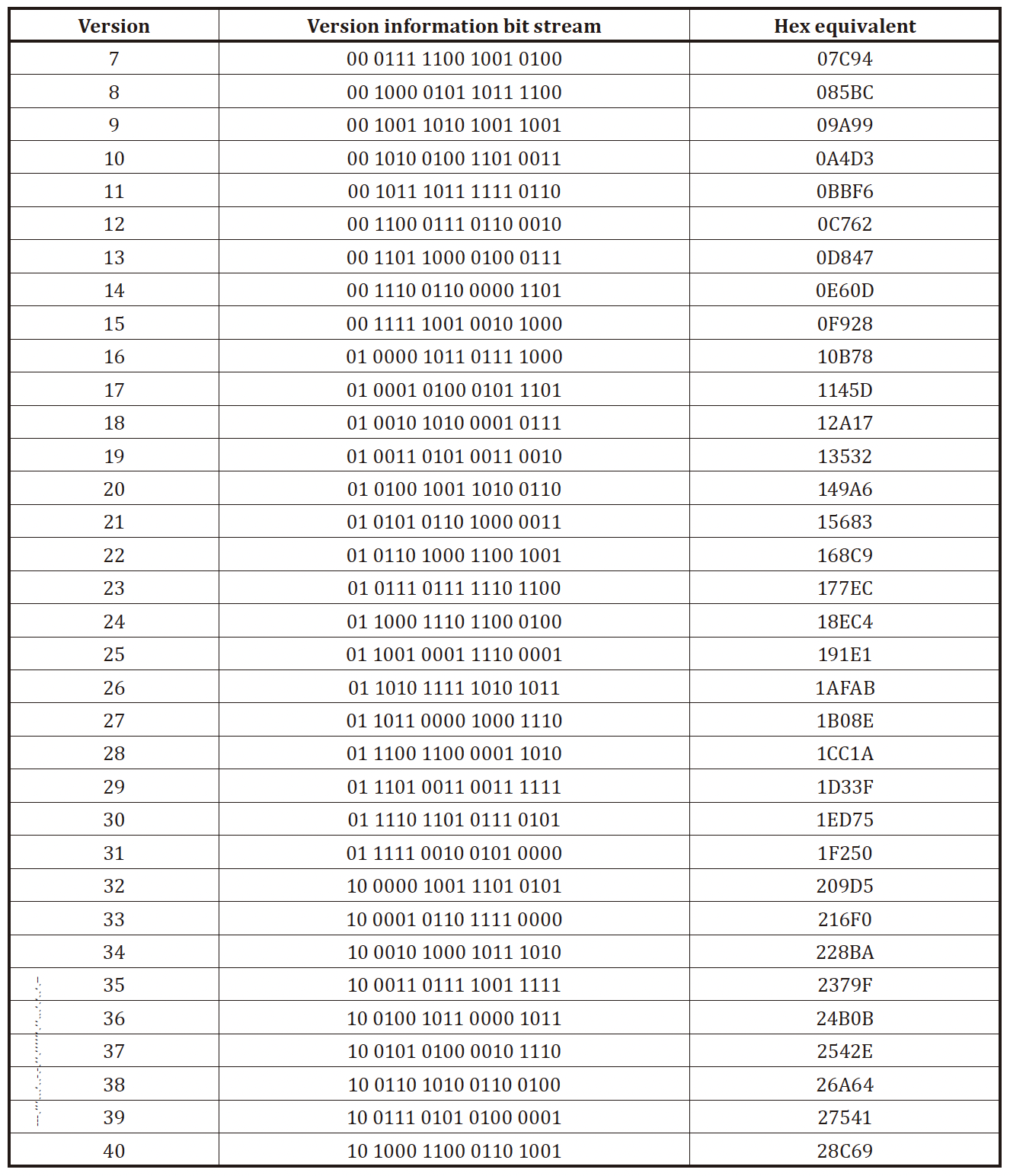
因为只有 34 个版本有版本信息,所以也就只有 34 种有效的版本信息序列,附录 D 的 Table D.1 中给出了完整的 34 个版本信息序列
和格式信息一样,纠错时对照表格选择相差比特数最小的即可。并且版本信息也只能纠正小于等于 3 个错误
填入二维码 ¶
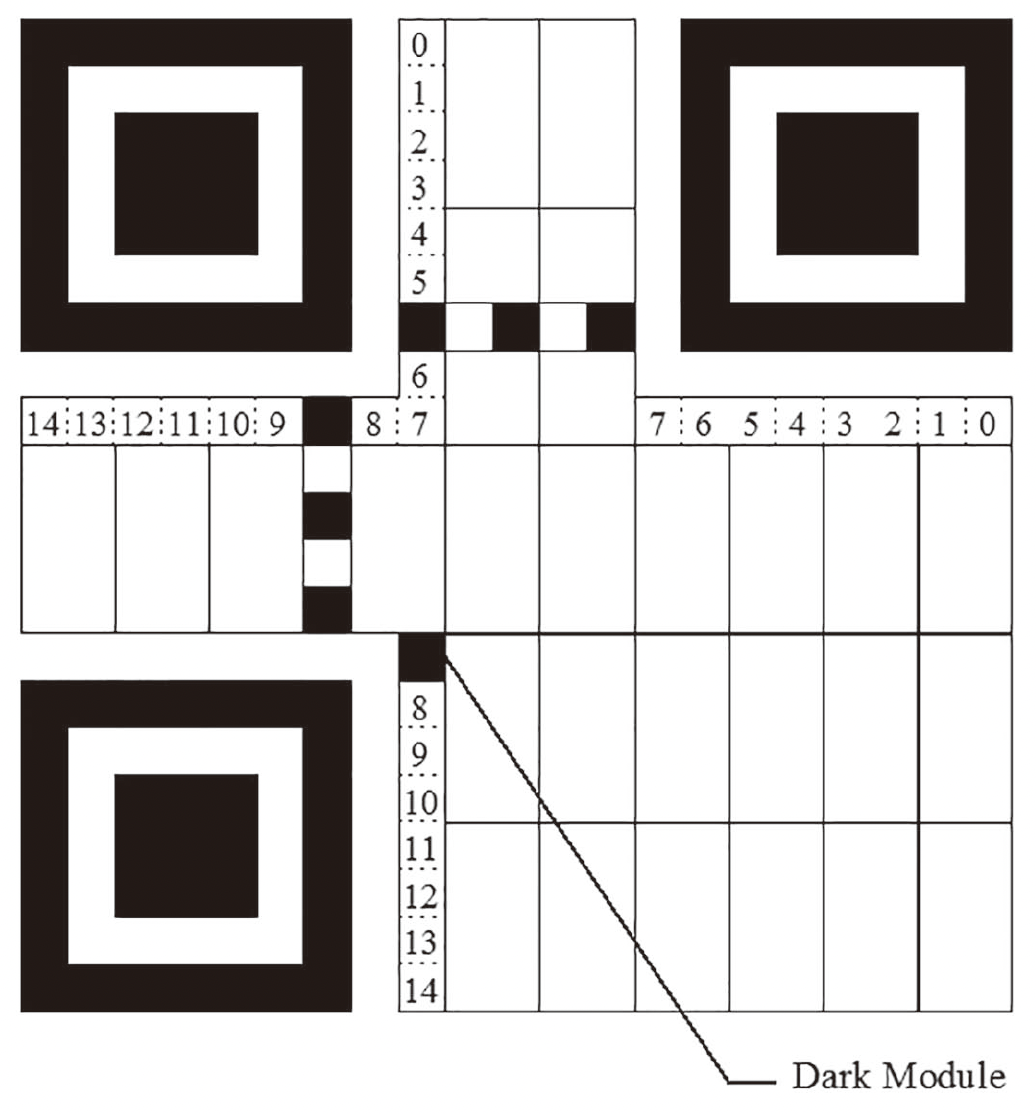
在版本 7 以上的二维码中已经预留出了两个 6*3 大小的区域,一个位于左下分割线的上方时序图案左侧,一个位于右上分割线左侧时序图案的上方
按照下图顺序填入即可:
解码(11、Annex B)¶
简要的解码过程:
- 定位并获取图像中的二维码,并把图像中的黑白块提取为 1 和 0
- 读取格式信息
- 释放掩码
101010000010010 - 进行纠错
- 如果纠错失败则将二维码镜面对称再尝试
- 释放掩码
- 读取版本信息(如果有的话)
- 读取格式信息中的掩码编号,并释放掩码
- 读取并恢复数据字和纠错字
- 纠错,如果检测到了错误就纠正
- 把数据字解码得到结果
纠错(Annex B)¶
Annex B 讲的纠错过程很简略,而且符号说明不全,很难看懂
去学了学 PGZ 解码:Reed–Solomon_error_correction#Peterson–Gorenstein–Zierler_decoder
设当前版本下每块中有 \(n\) 个字,\(k\) 个数据字,\(n-k\) 个纠错字,纠错容量为 \(\nu\)
首先定义原来的完整数据(即数据字和纠错字)从高位到低位为 \(c_{n-1},c_{n-2},\cdots,c_0\) ,对应多项式为:
而且根据纠错码生成原理,\(s(x)\) 可以被生成多项式 \(g(x)\) 整除,其中
所以 \(s(x)\) 也有根 \(s(\alpha^i)=0, i=0,1,\dots n-k-1\)
再设接收到的消息多项式(可能有错)为 \(r(x)\) ,误差多项式为 \(e(x)\) ,满足:
先设一共有 \(\nu\) 个错误,且每个错误的位置为 \(i_k,k=0,1,\dots \nu-1\),所以有:
最终的目标就是找到错误个数 \(\nu\),错误位置 \(i_k\),以及错误大小 \(e_{i_k}\)
计算典型值 ¶
首先定义典型值(syndromes)为把 \(\alpha^j\) 传入 \(r(x)\) 得到的值 \(S_j\),有:
此时如果得到的典型值都为 0,那说明没有错误
为了方便,再令 \(X_k=\alpha^{i_k},Y_k=e_{i_k}\),这样 \(X_k\) 也能用来定位错误,同时也有:
写成矩阵形式就是:
所以只要求得位置 \(X_k\) 就能得到错误大小,但是此时并不是线性的
错误定位多项式 ¶
定义一个错误定位多项式(error locator polynomial)\(\Lambda(x)\):
可以看出 \(\Lambda(X_k^{-1})=0\),所以对于 \(0\leq j\leq\nu-1\) 有:
所以把 \(k\) 从 \(0\) 到 \(\nu-1\) 累加起来也为 0:
然后转换为每项累加并提取出 \(\Lambda_i\):
根据典型值的定义有:
把 \(S_{j+\nu}\) 移到右边,并展开所有 \(j\) 可以得到矩阵形式:
此时是一个线性方程组,而且 \(S_i\) 全部已知,可以解得 \(\Lambda_i\)
得到错误位置和大小 ¶
此时多项式 \(\Lambda(x)\) 已经完全已知,所以可以求得其根(用 Chien search 算法在伽罗瓦域上求根)
再算其倒数即可得到 \(X_k\) ,然后可以寻找到错误位置 \(i_k\)
这时也就可以带入第一个方程组求得错误大小 \(Y_k\)(或者利用 Forney algorithm)
得到了 \(e(x)\) 后就可以根据 \(r(x)\) 算出原始信息 \(s(x)\) 了
创建日期: 2022年1月3日 21:02:29